1) ഒരു വൃത്തത്തിന്റെ ആധാരബിന്ദുവിന് ചുറ്റും 360ം കോൺ ഉണ്ടാകും.
2) മട്ടവും വൃത്തവും:- ഒരു വൃത്തത്തിലെ ഒരു വ്യാസത്തിന്റെ അഗ്രബിന്ദുക്കളിൽ നിന്നുള്ള വരകൾ വൃത്തത്തിലെ ഒരു ബിന്ദു(p)വിൽ ഉണ്ടാക്കുന്ന കോൺ 90ം ആയിരിക്കും.
3) ബിന്ദു വൃത്തത്തിന് അകത്തും പുറത്തും
ഒരു വൃത്തത്തിലെ വ്യാസാഗ്രങ്ങളിൽ നിന്നുള്ള വരകൾ വൃത്തത്തിനകത്തെ ഒരു ബിന്ദു (p)വിൽ ഉണ്ടാക്കുന്ന കോൺ 90ം യെക്കാൾ കൂടുതലാണ്. വൃത്തത്തിന്റെ പുറത്തെ ഒരു ബിന്ദുവിലുണ്ടാക്കുന്ന കോൺ 90ം യെക്കാൾ കുറവാണ്.
APB>90O APB<90O
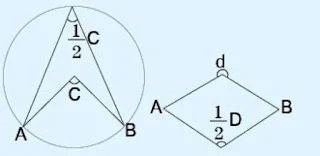
4) കോണും ചാപവും ഞാണും: വൃത്തത്തിലെ ഒരു ചാപം കേന്ദ്രത്തിലുണ്ടാക്കുന്ന കോണിന്റെ പകുതിയാണ് ആ ചാപം അതിന്റെ മറുചാപത്തിലെ ഒരു ബിന്ദുവിൽ ഉണ്ടാക്കുന്ന കോണിന്റെ അളവ്.
5) വൃത്തഖണ്ഡങ്ങൾ
ഒരു വൃത്തത്തിലെ ഏത് ഞാണും അതിനെ രണ്ട് ഭാഗങ്ങളാക്കും. ഈ ഭാഗങ്ങളാണ് വൃത്തഖണ്ഡങ്ങൾ
6) തുല്യമായ കോണുകൾ
ഒരേ വൃത്തഖണ്ഡത്തിലെ കോണുകളെല്ലാം തുല്യമാണ്
വൃത്തഖണ്ഡം Iൽ
p=q=r
വൃത്തഖണ്ഡം IIൽ
n=y=z
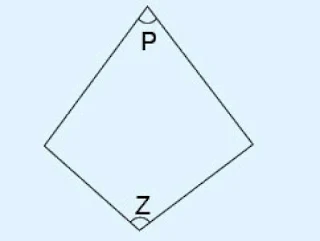
7) അനുപൂരകം: മറുഖണ്ഡങ്ങളിലെ കോണുകളുടെ തുക 180O ആണ്. അതായത് താഴെ കൊടുത്ത വൃത്തത്തിൽ p+z=180O ആയിരിക്കും.
8) ചക്രീയ ചതുർഭുജം: ഒരു ചതുർഭുജത്തിന്റെ മൂലകളെല്ലാം ഒരു വൃത്തത്തിലായ ചതുർഭുജമാണ് ചക്രീയ ചതുർഭുജം. അതിന്റെ എതിർകോണുകൾ അനുപൂരകങ്ങളായിരിക്കും.
cO+dO=360 (വൃത്തത്തിന്റെ കേന്ദ്രത്തിന് ചുറ്റുമുള്ള കോണളവ്)
ABE+ADE=c+d
=(cO+dO)
=x360 = 180
9) ബിന്ദു അകത്തും പുറത്തും: ഒരു ചതുർഭുജത്തിന്റെ മൂന്ന് മൂലകൾ ഒരുവൃത്തത്തിലും നാലാമത്തെ മൂല വൃത്തത്തിന് പുറത്തുമായാൽ ഈ മൂലയിലെയും എതിർമൂലയിലെയും കോണുകളുടെ തുക 180ം യിൽ കുറവും നാലാമത്തെ മൂല വൃത്തത്തിനകത്തായാൽ ഈ മൂലയിലെയും എതിർമൂലയിലെയും കോണുകളുടെ തുക 180O യിൽ കൂടുതലായിരിക്കും.
ADC + ABC < 180O ADC+ ABC > 180O
10. മുറിച്ചുകടക്കുന്ന ഞാണുകൾ (i) ഒരു വൃത്തത്തിലെ രണ്ട് ഞാണുകൾ വൃത്തത്തിനുള്ളിൽ മുറിച്ചുകടക്കുമ്പോൾ, രണ്ട് ഞാണുകളുടെയും ഭാഗങ്ങൾ തമ്മിലുള്ള ഗുണനഫലം തുല്യമാണ്.
PAC, PDB എന്നീ ത്രികോണങ്ങളിലെ കോണുകളെല്ലാം തുല്യമാണ്. അതിനാൽ വശങ്ങളുടെ അംശബന്ധവും തുല്യമാണ്.
... = ഇത് ഗുണനഫലരീതിയിൽ
PA x PB = P Cx PD
(ii) ഒരു വൃത്തത്തിലെ രണ്ടു ഞാണുകൾ വൃത്തത്തിനുള്ളിൽ മുറിച്ചുകടക്കുമ്പോൾ ഓരോ ഞാണിന്റെയും ഭാഗങ്ങൾ വശങ്ങളായ ചതുരങ്ങൾക്ക് ഒരേ പരപ്പളവാണ്.
11). ചതുരത്തിന്റെ പരപ്പളവ് മാറാതെ മറ്റൊരു ചതുരം. ചതുരത്തിന്റെ പരപ്പളവ് =ab
ab=(a+c)x
or
8cm2 പരപ്പളവുള്ള സമചതുരം വരയ്ക്കുക.
or
ചതുരം APCE യുടെ പരപ്പിന് തുല്യമാണ് സമചതുരം PQRD യുടെ പരപ്പളവ്. PQRD സമചതുരത്തിന്റെ പരപ്പ് 8cm2
13. ത്രികോണപരപ്പിന് തുല്യമായ ചതുരം വശങ്ങളുടെ നീളം 4cm, 5cm, 6cm ആയ ത്രികോണം നിർമിച്ച് ഇതേ പരപ്പളവുള്ള ചതുരം വരയ്ക്കുക.