Kerala Plus One Maths Notes Chapter 2 Relations and Functions

 

 I. Cartesian Product or Cross Product:

The Cartesian product between two sets A and B is denoted by A × B is the set of all ordered pairs of elements from A and B.
ie; A × B = {(a, b): a ∈ A, b ∈ B}

Properties:

1. In general A × B ≠ B × A, but if A = B, A × B = B × A.
2. n(A × B) = n(A) × n(B)
3. n(A × B) = n(B × A)

II. Relations:
A relation R from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.

Representation of a relation:

1. Roster form
2. Set builder form
3. Arrow diagram.

Universal relation from A to B is A × B.

Empty relation from A to B is empty set φ.

A relation in A is a subset of A × A.

The number of relation that can be written from A to B if n(A) = p, n(B) = q is 2pq.

Domain: It is the set of all first elements of the ordered pairs in a relation.

Range: It is the set of all second elements of the ordered pairs in a relation.
If R: A → B, then R(R) ⊆ B.

Co-domain: If R: A → B, then Co-domain of R = B.

III. Functions:
A relation f from A to B (f : A → B) is said to be a function if every element of set A has one and only one image in set B.

If f : A → B is a function defined by f(x) = y.

1. The image of x = y
2. The pre-image of y = x
3. Domain of f = {x ∈ A : f(x) ∈ B}
4. Range of f = {f(x) : x ∈ D(f)}
5. If f : A → B, then n(f) = n(B)n(A)

IV. Some Important Functions

Identity function: A function f : R → R defined by f(x) = x. Here D(f) = R, R(f) = R.
The graph of the above function is a straight line passing through the origin which makes 45 degrees with the positive direction of the x-axis.

Constant function: A function f : R → R defined by f(x) = c, where c is a constant.
Here D(f ) = R, R(f) = {c}.
The graph of the above function is a straight line parallel to the x-axis.

Polynomial function: A function f : R → R defined by
f(x) = a0 + a1x + ….. + anxn, where n is a no-negative integer and a0, a1, …., an ∈ R.

Rational function: A function f: R → R defined by f(x)=p(x)q(x), where p(x), q(x) are functions of x defined in a domain, where q(x) ≠ 0

Modulus function: A function f: R → R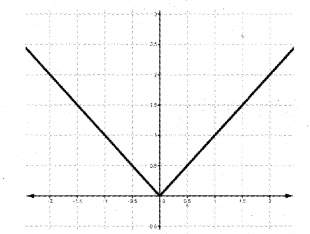

Here D(f) = R, R(f) = [0, ∞).
The graph of the above function is ‘V’ shaped with a corner at the origin.

Signum function: A function f: R → R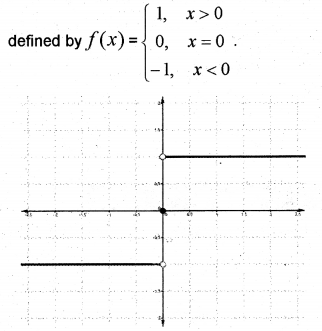

Here D(f) = R, R(f) = {-1, 0, 1}.
The graph of the above function has a break at x = 0.

Greatest integer function f: R → R defined by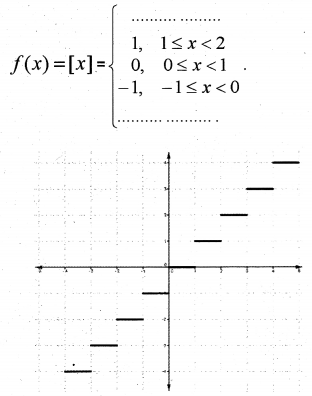

Here D(f) = R, R(f) = Z.
The graph of the above function has broken at all integral points.

V. Algebra of Functions

Let f : X → R and g : X → R be any two real functions, where X ⊂ R. Then, we define (f + g) : X → R by (f + g)(x) = f(x) + g(x) for all x ∈ X

Let f : X → R and g : X → R be any two real functions, where X ⊂ R. Then, we define (f – g) : X → R by (f – g)(x) = f(x) – g(x) for all x ∈ X

Let f : X → R be a real-valued function and k be a scalar. Then, the product kf : X → R by (kf)(x) = kf (x) for all x ∈ X

Let f : X → R and g : X → R be any two real functions, where X ⊂ R . Then, we define fg : X → R by fg(x) = f(x) × g(x) for all x ∈ X

Let f : X → R and g : X → R be any two real functions, where X ⊂ R. Then, we define fg : X → R by
(fg)(x)=f(x)g(x) for all x ∈ X

We hope the Plus One Maths Notes Chapter 2 Relations and Functions help you. If you have any query regarding Kerala Plus One Maths Notes Chapter 2 Relations and Functions, drop a comment below and we will get back to you at the earliest.