Kerala Plus One Physics Notes Chapter 12 Thermodynamics

 

Summary

Thermodynamics is the branch of Physics that deals with concept of heat and temperature, their inter-conversions and other forms of energy. In thermodynamics state of system is specified by macroscopic variables such as pressure, temperature, volume, mass, composition… etc.

Thermo Equilibrium
Thermodynamic equilibrium:
A system is said to be in thermodynamic equilibrium if the macroscopic variables used to describe the system does not change with time.
Eg: Agas enclosed in a rigid container (characterized by P, V, T, m, and composition) The equilibrium of a thermodynamic system depends on surroundings and nature of wall that separates the system from surroundings. The wall can be

• Adiabatic wall – It does not allow flow of heat (energy).
• Diathermic wall – It allows the flow of heat (so that it can comes to thermal equilibrium).

Zeroth Law Of Thermodynamics
Zeroth law of thermodynamics gives concept of temperature. R.H Fowler formulated this law in 1931. According to Zeroth law of thermodynamics, the systems in thermal equilibrium with a third system separately are in thermal equilibrium with each other.

Let A & B are in thermal equilibrium with each other. If they are separately in thermal equilibrium with C, then the three systems are in thermal equilibrium
(TA = TB = TC).

Heat, Internal Energy And Work
Internal Energy (U):
internal energy of a gas is the sum of potential energy and kinetic energy (translational kinetic energy, rotational kinetic energy and vibrational energy) Internal energy is a thermodynamic variable and hence it depends on state of the thermodynamic system.

Heat and Work:
The internal energy of a system can be changed either by heat or by work. Heat is energy transfer between a system and surroundings due to temperature difference. Work is mode of energy transfer brought about by means like moving piston (it is not due to temperature difference)

First Law Of Thermodynamics
According to first law of thermodynamics, heat supplied to a system is used to increase its internal energy and to do work.
If ∆Q is heat supplied to the system, ∆W is work done by the system and Au is change in internal energy, then ∆Q = ∆U + AW
Note:

• If the entire heat supplied to the system is used to do work, then ∆Q = ∆W
• The work done against constant pressure, ∆W = P∆V, ∆Q = ∆U + P∆V.

Specific Heat Capacity
Molar specific heat capacity of solid:
Consider a solid consisting of N atoms. Each atom have an average energy 3KBT, where KB is Botlzman constant. Total energy for one,mole
U = 3KBT × NA
NA is avagadro number.
At constant pressure, ∆Q = ∆U + P∆V
For solid ∆V is negligible ∆Q = ∆U
Molar specific heat capacity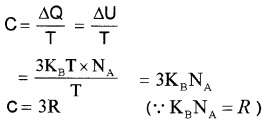

Thus molar specific heat capacity of solids is found to be 3R. But at low-temperature molar, specific heat capacity is not a constant.
Specific heat capacity of water:
The specific heat capacity of water is 4186 J Kg-‘K1. But the specific heat capacity of water changes with temperature as shown.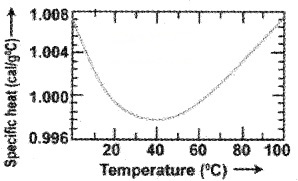

Mayor’s Relation; Cp – Cv = R
If molar specific heat capacity of constant pressure is Cp and that at constant volume is Cv then Cp – Cv = R, for an ideal gas.
Proof:
According to 1st law of thermodynamics
∆Q = ∆U + P∆V
If ∆Q heat is absorbed at constant volume (∆V = 0)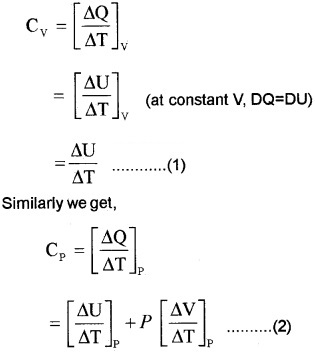

From ideal gas equation for one mole PV = RT Differentiating w.r.t. temperature (at constant pressure)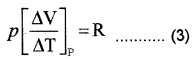

Substituting in equation (2)

Equation (4) – Equation (1), we get Cp – Cv = R.

Thermodynamic State Variable And Equation Of State
Extensive and Intensive variables:
Thermodynamic variables can be extensive or intensive. Extensive variables depend on size of the system.
Eg: mass, internal energy, volume.
Intensive variables are independent of size of system.
Eg: Pressure, temperature, density.
Equation of state:
The relation between state variables of a system is called equation of state. For an ideal gas equation of state is PV = µRT

Thermodynamic process
1. Quasi-static process:
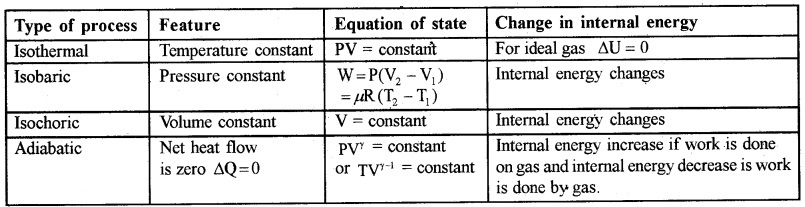
The thermodynamic process in which thermodynamic variables (P, V, T… etc) changes so slowly that the system remains in thermal and mechanical equilibrium is called quasi-static (nearly static) process. In quasi-static process change in temperature or pressure will be infinitesimally small. The different types of quasi static process are listed in the above table.

2. Work done in isothermal process:
For an isothermal process, the equation of state is
PV = constant = µRT
P = μRTV
Let a system undergoes an isothermal process at temperature T, from the state (P1, V1) to (P2, V2). Let ‘DV’ be a small charge in volume due to pressure P.
Then work done (for ∆V)
∆W = P∆V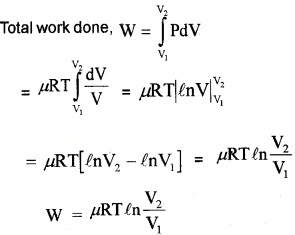

3. Work done by adiabatic process:
Let an ideal gas undergoes adiabatic charge from (P1, V1) to (P2, V2). The equation for adiabatic charge is PVγ = constant = k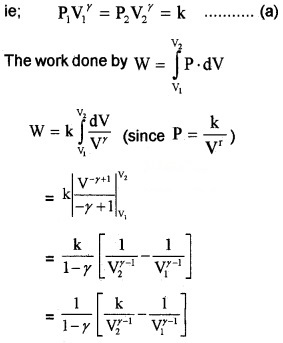

from equation (a) P1V1γ = P2V2γ = k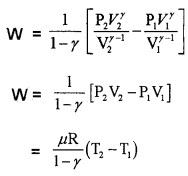

Substituting ideal gas equation.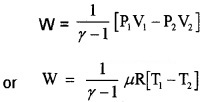

Note:

1. The graph connecting P and V of isothermal process is called isotherm.
2. In adiabatic process
   • T1 < T2, then work is done on gas (w < 0)
   • T1 > T2, then work is done by gas (w > 0)
3. For Isothermal process
   • V1 < V2, w > 0 work is done by gas
   • V1 > V2, w < 0 work is done on gas.
4. In isochoric process no work is done on or by gas because volume is constant.

Cyclic process:
In cyclic process, the system returns to its initial state such that change in internal energy is zero. The P – V diagram for cyclic process will be closed loop and area of this loop gives work done or heat absorbed by system.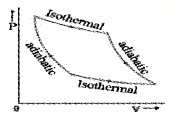

Heat Engines
Heat engines converts heat energy into mechanical energy. Heat engine is a device by which a system is made to undergo a cyclic process that results in conversion of heat to work.
Heat engines consists of:

1. Working substance (the system which undergoes cyclic process) eg: mixture of fuel vapor and air in diesel engine, steam in steam engine.
2. An external reservoir at a high temperature (T1) – it is the source of heat.
3. An external reservoir at low temperature (T2) or sink

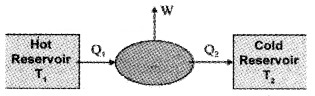
Working:
The working substances absorbs an energy Q1 from source reservoir at a temperature T1. It undergoes cyclic process and releases heat Q2 to cold reservoir. The change in heat (Q1 – Q2) is converted into work (mechanical energy).
Efficiency of heat engine (η):
The efficiency of heat engine is the ratio of work done to input heat.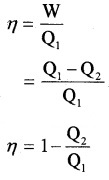

Note:

• Q2 = 0, η = 1. When entire heat input is converted into work heat engine is 100% efficient. But practically 100% efficiency cannot be achieved. It is limited by second law of thermodynamics.
• Heat engine can be external combustion engine or internal combustion engine.

In external combustion engine, the fuel (system) is heated by external furnace.
Eg.: Steam engine.
In internal combustion engine, fuel is heated internally by exothermic chemical reactions.
Eg: Diesel engine, Patrol engine.

Refrigerators And Heat Pumps
Refrigerator is reverse of heat engine, the device used to cool a portion of space (inside a chamber) is refrigerator. The device used to pump heat into a portion of space (to warm-up room) is called heat pump.

In both devices, the working substance absorbs heat Q2 from cold reservoir at temperature T2. Some external work (by compression of gas by electric means) is done on it and heat Q1 is supplied to hot reservoir at T1.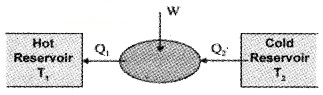

The working cycle of refrigerator:
In refrigerator the working substance is a gas (freon)

Step1: The gaseous working substance is converted into vapor- liquid mixture at lower temperature (T2)
Step 2: The cold fluid absorbs heat from region to be cooled (cold reservoir) and convert it into vapor.
Step 3: The vapor is heated by external work.
Step 4: The vapor release heat to surroundings and then comes to initial temperature T2.

The coefficient of performance (α):
The coefficient of performance of refrigerator is defined as
α = Q2W
where Q2 is heat extracted from cold reservoir and W is work done on system.
Note:

• The working substance in refrigerator is termed as refrigerant.
• For heat engine η can not exceed 1. But α can be greater than one.

Second law of Thermo dynamics
Kelvin – Plank statement:
No process is possible whose sole result is the absorption of heat from a reservoir and complete conversion of heat into work.
Clausius statement:
No process is possible whose sole result is the transfer of heat from a colder object to hotter object.

Reversible And Irreversible Processes
A themodynamic process is said to be reversible if the process can bring both system and surrounding back to the original state without any change.

A reversible thermodynamic process is ideal case. Most thermodynamic processes are irreversible because the process involves dissipative effects like friction, viscous force etc. and during such process, system passes through non-equilibrium states.
Note: Condition for a thermodynamic process to be reversible is

1. Quasi static
2. non-dissipative

Question 1.
What is the importance of reversibility in thermodynamics?
Answer:
The main concern of thermodynamics is the efficiency with which heat can be converted into work. According to second law of thermodynamics, the efficiency can not be 100%. The heat engine can have highest efficiency only if the cyclic process is reversible.

Carnot’S Engine
Carnot’s theorem:
Sadi carnot proposed Carnot’s theorem. According to Carnot’s theorem

1. No engine operating between two temperature can have efficiency more than that of Carnot’s engine,
2. The efficiency of Carnot’s engine is independent of nature of working substance.

Carnot’s engine:
A reversible heat engine operating between two temperatures is called Carnot’s engine.
Carnot’s cycle:
The Carnot cycle consists of two isothermal processes and two adiabatic processes.

The cylindar is placed on the source. The gas expands and temperature increases. This is the first stroke of the heat engine. The expansion is an isothermal expansion.

During this expansion the working substance originally at the state A (P1, V1, T1) has new variable (P2, V2, T1). The variation A to B is shown byAB in v-p graph.

During the second stroke, the cylinder is placed on the stand and the gas is allowed to expand further and reaches the state C. The new Co-ordinate are (P3, V3, T2).

This expansion is adiabatic expansion. The third stroke is carried out when cylinder is placed on the zink. The cylinder undergoes for isothermal compression and coordinate becomes (P4, V4, T2).

In the fourth and final stroke, the cylinder is placed on the non conducting stand. The gas is compressed back to state A. This is adiabatic compression.

1. The work done by gas in one Carnot cycle
Step 1: Isothermal expansion : The gas absorbs heat Q, from hot reserviorand undergoes Isothermal expansion.
[(P1, V1, T1) → (P2, V2, T2)]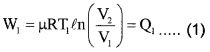

Step 2: Adiabatic expansion
[(P2, V2, T1) → (P3, V3, T2)]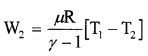

Step 3: Isothermal compression: The gas releases heat Q2 to cold reservoir at T2.
[(P3, V3, T2) → (P4, V4, T2)]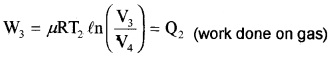

Step 4: Adiabatic compression
[(P4, V4, T2) → (P1, V1, T1)]

2. Efficiency of Carnot’s engine: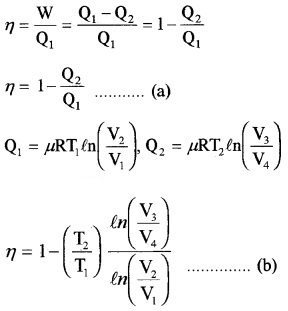

In adiabatic expansion from
(P2, V2, T1) to (P3, V3, T2)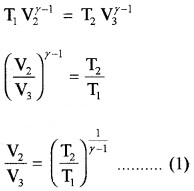

In adiabatic compression
(P4, V4, T2) to (P1, V1, T1)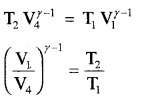

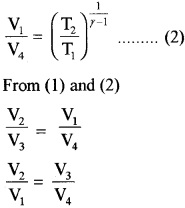
Thus equation (b) becomes η = 1 – T2T1 ……..(3)
Comparing this with equation (a)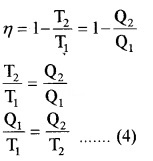

Note:

• The equation
• Shows that efficiency of heat engine is independent of nature of working substance